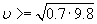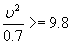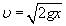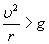Почему не падает вращающийся волчок?
Из тысяч людей, забавлявшихся в детстве с волчком, не многие смогут правильно ответить на этот вопрос. Как, в самом деле, объяснить то, что вращающийся волчок, поставленный отвесно или даже наклонно, не опрокидывается, вопреки всем ожиданиям? Какая сила удерживает его в таком, казалось бы, неустойчивом положении? Разве тяжесть на него не действует?Здесь имеет место весьма любопытное взаимодействие сил. Теория волчка непроста, и углубляться в нее мы не станем. Наметим лишь основную причину, вследствие которой вращающийся волчок не падает.
На рис. 26 изображен волчок, вращающийся в направлении стрелок. Обратите внимание на часть А его ободка и на часть В, противоположную ей. Часть А стремится двигаться от вас, часть В – к вам. Проследите теперь, какое движение получают эти части, когда вы наклоняете ось волчка к себе. Этим толчком вы заставляете часть А двигаться вверх, часть В – вниз; обе части получают толчок под прямым углом к их собственному движению. Но так как при быстром вращении волчка окружная скорость частей диска очень велика, то сообщаемая вами незначительная скорость, складываясь с большой круговой скоростью точки, дает равнодействующую, весьма близкую к этой круговой, – и движение волчка почти не меняется. Отсюда понятно, почему волчок как бы сопротивляется попытке его опрокинуть. Чем массивнее волчок и чем быстрее он вращается, тем упорнее противодействует он опрокидыванию.

Рисунок 26. Почему волчок не падает?
Сущность этого объяснения непосредственно связана с законом инерции. Каждая частица волчка движется по окружности в плоскости, перпендикулярной к оси вращения. По закону инерции частица в каждый момент стремится сойти с окружности на прямую линию, касательную к окружности. Но всякая касательная расположена в той же плоскости, что и сама окружность; поэтому каждая частица стремится двигаться так, чтобы все время оставаться в плоскости, перпендикулярной к оси вращения. Отсюда следует, что все плоскости в волчке, перпендикулярные к оси вращения, стремятся сохранить свое положение в пространстве, а поэтому и общий перпендикуляр к ним, т. е. сама ось вращения, также стремится сохранить свое направление.
Не будем рассматривать всех движений волчка, которые возникают при действии на него посторонней силы. Это потребовало бы чересчур подробных объяснений, которые, пожалуй, покажутся скучными. Я хотел лишь разъяснить причину стремления всякого вращающегося тела сохранять неизменным направление оси вращения.
Этим свойством широко пользуется современная техника. Различные гироскопические (основанные на свойство волчка) приборы – компасы, стабилизаторы и др. – устанавливаются на кораблях и самолетах.
Таково полезное использование простой, казалось бы, игрушки.
Искусство жонглеров
Многие удивительные фокусы разнообразной программы жонглеров основаны тоже на свойстве вращающихся тел сохранять направление оси вращения. Позволю себе привести выдержку из увлекательной книги английского физика проф. Джона Перри «Вращающийся волчок».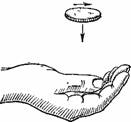
Рисунок 28. Как летит монета, подброшенная с вращением.
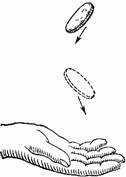
Рисунок 29. Монета, подброшенная без вращения, падает в случайном положении.
«Однажды я показывал некоторые из моих опытов перед публикой, пившей кофе и курившей табак в великолепном помещении концертного зала „Виктория“ в Лондоне. Я старался заинтересовать моих слушателей, насколько мог, и рассказывал о том, что плоскому кольцу надо сообщить вращение, если его желают бросить так, чтобы можно было наперед указать, куда оно упадет; точно так же поступают, если хотят кому-нибудь бросить шляпу так, чтобы он мог поймать этот предмет палкой. Всегда можно полагаться на сопротивление, которое оказывает вращающееся тело, когда изменяют направление его оси. Далее я объяснял моим слушателям, что, отполировав гладко дуло пушки, никогда нельзя рассчитывать на точность прицела; вследствие этого теперь делают нарезные дула, т. е. вырезают на внутренней стороне дула пушек спиралеобразные желоба, в которые приходятся выступы ядра или снаряда, так что последний должен получить вращательное движение, когда сила взрыва пороха заставляет его двигаться по каналу пушки. Благодаря этому снаряд покидает пушку с точно определенным вращательным движением.
Это было все, что я мог сделать во время этой лекции, так как я не обладаю ловкостью в метании шляп или дисков. Но после того, как я закончил свою лекцию, на подмостки выступили два жонглера, – и я не мог пожелать лучшей иллюстрации упомянутых выше законов, нежели та, которую давал каждый отдельный фокус, показанный этими двумя артистами. Они бросали друг другу вращающиеся шляпы, обручи, тарелки, зонтики… Один из жонглеров бросал в воздух целый ряд ножей, ловил их опять и снова подбрасывал с большой точностью вверх; моя аудитория, только что прослушав объяснение этих явлений, ликовала от удовольствия; она замечала вращение, которое жонглер сообщал каждому ножу, выпуская его из рук так, что мог наверное знать, в каком положении нож снова вернется к нему. Я был тогда поражен, что почти все без исключения жонглерские фокусы, показанные в тот вечер, представляли иллюстрацию изложенного выше принципа».
Новое решение колумбовой задачи
Свою знаменитую задачу о том, как поставить яйцо, Колумб решил чересчур просто: надломил его скорлупу. Такое решение, в сущности, неверно: надломив скорлупу яйца, Колумб изменил его форму и, значит, поставил не яйцо, а другое тело; ведь вся суть задачи в форме яйца: изменяя форму, мы заменяем яйцо другим телом. Колумб дал решение не для того тела, для которого оно искалось.
А между тем можно решить задачу великого мореплавателя, нисколько не изменяя формы яйца, если воспользоваться свойством волчка; для этого достаточно только привести яйцо во вращательное движение вокруг его длинной оси, – и оно будет, не опрокидываясь, стоять некоторое время на тупом или даже на остром конце. Как это сделать – показывает Рисунок : яйцу придают вращательное движение пальцами. Отняв руки, вы увидите, что яйцо продолжает еще некоторое время вращаться стоймя: задача решена.
Для опыта необходимо брать непременно вареные яйца. Это ограничение не противоречит условию колумбовой задачи: предложив ее, Колумб взял яйцо тут же со стола, а к столу, надо полагать, поданы были не сырые яйца. Вам едва ли удастся заставить стоймя вращаться яйцо сырое, потому что внутренняя жидкая масса является в данном случае тормозом. В этом, между прочим, состоит простой способ отличать сырые яйца от сваренных вкрутую – прием, известный многим хозяйкам.
«Уничтоженная» тяжесть
«Вода не выливается из сосуда, который вращается, – не выливается даже тогда, когда сосуд перевернут дном вверх, ибо этому мешает вращение», – писал две тысячи лет назад Аристотель. На рис. 32 изображен этот эффектный опыт, который, без сомнения, многим знаком: вращая достаточно быстро ведерко с водой, как показано на рисунке, вы достигаете того, что вода не выливается даже в той части пути, где ведерко опрокинуто вверх дном.В обиходе принято объяснять это явление «центробежной силой», понимая под нею ту воображаемую силу, которая будто бы приложена к телу и обусловливает стремление его удалиться от центра вращения. Этой силы не существует: указанное стремление есть не что иное, как проявление инерции, а всякое движение по инерции осуществляется без участия силы. В физике под центробежной силой разумеют нечто иное, а именно – ту реальную силу, с какой вращающееся тело натягивает удерживающую его нить или давит на свой криволинейный путь. Сила эта приложена не к движущемуся телу, а к препятствию, мешающему ему двигаться прямолинейно: к нити, к рельсам на кривом участке пути и т. п.
Обращаясь к вращению ведерка, попытаемся разобраться в причине этого явления, не прибегая вовсе к двусмысленному понятию «центробежной силы». Зададим себе вопрос: куда направится струя воды, если в стенке ведерка сделать отверстие? Не будь силы тяжести, водяная струя по инерции направилась бы по касательной АК к окружности АВ (рис. 32). Тяжесть же заставляет струю снижаться и описывать кривую (параболу АР). Если окружная скорость достаточно велика, эта кривая расположится вне окружности АВ. Струя обнаруживает перед нами тот путь, по которому при вращении ведерка двигалась бы вода, если бы не препятствовало надавливающее на нее ведерко. Теперь понятно, что вода вовсе не стремится двигаться отвесно вниз, а потому и но выливается из ведерка. Она могла бы вылиться из него лишь в том случае, если бы ведерко было обращено отверстием в направлении его вращения.
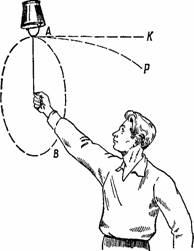
Вычислите теперь, с какой скоростью надо в этом опыте вращать ведерко, чтобы вода из него не выливалась вниз. Скорость эта должна быть такова, чтобы центростремительное ускорение вращающегося ведерка было не меньше ускорения силы тяжести: тогда путь, по которому стремится двигаться вода, будет лежать вне окружности, описываемой ведерком, и вода нигде от ведерка не отстанет. Формула для вычисления центростремительного ускорения W такова;
W=v2/R,
где v – окружная скорость, R – радиус кругового пути. Так как ускорение тяжести на земной поверхности g = 9,8 м/сек2, то имеем неравенство v2/R»= 9,8. Если положить R равным 70 см, то
Легко рассчитать, что для получения такой окружной скорости надо делать рукой около полутора оборотов в секунду. Подобная быстрота вращения вполне достижима, и опыт удается без труда.
Способностью жидкости прижиматься к стенкам сосуда, в котором она вращается вокруг горизонтальной оси, пользуются в технике для так называемого центробежного литья. При этом имеет существенное значение то, что неоднородная жидкость расслаивается по удельному весу: более тяжелые составные части располагаются дальше от оси вращения, легкие занимают место ближе к оси. Вследствие этого все газы, содержащиеся в расплавленном металле и образующие так называемые «раковины» в литье, выделяются из металла во внутреннюю, полую часть отливки. Изделия, изготовленные таким способом, получаются плотные и свободные от раковин. Центробежное литье дешевле обычного литья под давлением и не требует сложного оборудования.
Вы в роли Галилея
Для любителей сильных ощущений иногда устраивается весьма своеобразное развлечение – так называемая «чертова качель». Имелась такая качель и в Ленинграде. Мне не пришлось самому на ней качаться, а потому приведу здесь ее описание из сборника научных забав Федо:«Качель подвешена к прочной горизонтальной перекладине, перекинутой через комнату на известной высоте над полом. Когда все сядут, особо приставленный к этому служитель запирает входную дверь, убирает доску, служившую для входа, и, заявив, что он сейчас даст возможность зрителям сделать небольшое воздушное путешествие, начинает легонько раскачивать качель. Вслед за тем он садится назади качели, подобно кучеру на запятках, или совсем выходит из зала.
Между тем размахи качели становятся все больше и больше; она, по-видимому, поднимается до высоты перекладины, потом переходит за нее, выше и выше и, наконец, описывает полный круг. Движение ускоряется все заметнее, и качающиеся, хотя по большей части уже предупрежденные, испытывают несомненные ощущения качания и быстрого движения; им кажется, что они несутся вниз головой в пространстве, так что невольно хватаются за спинки сидений, чтобы не упасть.
Но вот размахи начинают уменьшаться; качель более не поднимается уже на высоту перекладины, а еще через несколько секунд останавливается совершенно.
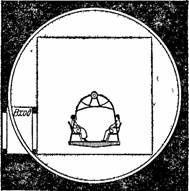
На самом же доле качель все время висела неподвижно, пока продолжался опыт, а сама комната, с помощью очень несложного механизма, обращалась мимо зрителей вокруг горизонтальной оси. Разного рода мебель прикреплена к полу или стенам зала; лампа, припаянная к столу так, что она, по-видимому, легко может перевернуться, состоит из электрической лампочки накаливания, скрытой под большим колпаком. Служитель, который, по-видимому, раскачивал качель, давая ей легкие толчки, в сущности, сообразовал их с легкими колебаниями зала и делал только вид, что раскачивает. Вся обстановка способствует полному успеху обмана».
Секрет иллюзии, как видите, прост до смешного. И все-таки, если бы теперь, уже зная, в чем дело, вы очутились на «чертовой качели», вы неизбежно поддались бы обману. Такова сила иллюзии!
Помните стихотворение Пушкина «Движение»?
– Движенья нет, – сказал мудрец брадатый.
Другой смолчал – и стал пред ним ходить.
Сильнее бы не мог он возразить.
Хвалили все ответ замысловатый.
Но, господа, забавный случай сей
Другой пример на память мне приводит:
Ведь каждый день над нами Солнце ходит,
Однако ж прав упрямый Галилей!
Среди пассажиров качели, не посвященных в ее секрет, вы были бы своего рода Галилеем – только наоборот: Галилей доказывал, что Солнце и звезды неподвижны, а кружимся, вопреки очевидности, мы сами; вы же будете доказывать, что неподвижны мы, а вся комната вертится вокруг нас. Возможно, что вам пришлось бы при этом испытать и печальную участь Галилея; на вас смотрели бы, как на человека, спорящего против очевидных вещей…
Мой спор с вами
Доказать свою правоту вам будет не так легко, как вы, может быть, полагаете. Вообразите, что вы в самом деле очутились на «чертовой качели» и хотите убедить ваших соседей, что они заблуждаются. Предлагаю вам вступить в этот спор со мной. Сядем с вами на «чертову качель», дождемся момента, когда, раскачавшись, она начнет, по-видимому, описывать полные круги, и заведем диспут о том, что кружится: качель или вся комната? Прошу только помнить, что во время спора мы но должны покидать качели; все необходимое захватим с собой заблаговременно.Вы. Как можно сомневаться в том, что мы неподвижны, а вертится комната! Ведь если бы нашу качель в самом деле опрокинуть вверх дном, то мы с вами не повисли бы вниз головой, а выпали бы из нес. Но мы не падаем. Значит, вертится не качель, а комната.
Я. Однако вспомните, что вода из быстро кружащегося ведерка не выливается, хотя оно и опрокидывается вверх дном (стр. 55). Велосипедист в «чертовой петле» (см. далее, стр. 65) также не падает, хотя и едет вниз головой.
Вы. Если так, то вычислим центростремительное ускорение и убедимся, достаточно ли оно для того, чтобы мы не выпали из качели. Зная наше расстояние от оси вращения и число оборотов в секунду, мы легко определим по формуле…
Я. Не трудитесь вычислять. Устроители «чертовой качели», зная о нашем споре, предупредили меня, что число оборотов будет вполне достаточно, чтобы явление объяснялось по-моему. Следовательно, вычисление не решит нашего спора.
Вы. Однако я не потерял надежды вас переубедить. Видите, вода из этого стакана не выливается на пол… Впрочем, вы и тут сошлетесь на опыт с вращающимся ведерком. Хорошо же: я держу в руке отвес, – он все время направлен к нашим ногам, т. е. вниз. Если бы вертелись мы, а комната оставалась неподвижной, отвес был бы все время обращен к полу, т. е. вытягивался бы то к нашим головам, то вбок.
Я. Ошибаетесь: если мы вертимся с достаточной скоростью, то отвес все время должен отбрасываться от оси вдоль радиуса вращения, т. с. к нашим ногам, как мы и наблюдаем.
Финал нашего спора
Теперь позвольте вам посоветовать, как одержать победу в этом споре. Надо взять с собою на «чертову качель» пружинные весы, положить на их чашку гирю, например в 1 кг, и следить за положением указателя: он все время будет показывать один и тот же означенный на гире вес, именно – один килограмм. Это и есть доказательство неподвижности качели.В самом деле: если бы мы вместе с пружинными весами описывали круги около оси, то на гирю, кроме силы тяжести, действовал бы также центробежный эффект, который в нижних точках пути увеличивал бы вес гири, а в верхних уменьшал бы его; мы должны были бы замечать, что гиря то становится тяжелее, то почти ничего не весит. А раз этого не замечается, значит, вращается комната, а не мы.
В «заколдованном» шаре
Один предприниматель в Америке устроил для развлечения публики очень забавную и поучительную карусель в форме шарообразной вращающейся комнаты. Люди внутри нее испытывают такие необыкновенные ощущения, какие мы считаем возможными разве только во сне или в волшебной сказке.Вспомним сначала, что испытывает человек, стоящий на быстро вращающейся круглой платформе.
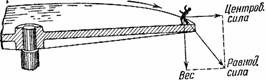
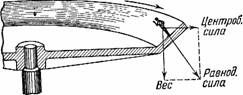
Вращательное движение стремится отбросить человека наружу; чем дальше стоите вы от центра, тем сильнее будет клонить и тянуть вас наружу. Если закроете глаза, вам будет казаться, что вы стоите не на горизонтальном полу, а на наклонной плоскости, на которой с трудом сохраняете равновесие. Это станет понятно, когда рассмотрим, какие силы действуют здесь на наше тело (рис. 34). Действие вращения увлекает паше тело наружу, тяжесть тянет вниз; оба движения, складываясь по правилу параллелограмма, дают результирующее действие, которое наклонено вниз. Чем быстрее вращается платформа, тем это результирующее движение больше и направляется более отлого.
Представьте же себе теперь, что край платформы загнут вверх и вы стоите на этой отогнутой наклонной части (рис. 35). Если платформа неподвижна, вы в таком положении не удержитесь, а сползете или даже опрокинетесь. Другое дело, если платформа вращается: тогда эта наклонная плоскость станет для вас, при известной скорости, как бы горизонтальной, потому что результирующее обоих увлекающих вас движений направится тоже наклонно, под прямым углом к отогнутой части платформы.
Если вращающейся платформе придать такую кривизну, чтобы при определенной скорости ее поверхность была в каждой точке перпендикулярна к результирующей, то помещенный на пол человек будет чувствовать себя во всех ее точках, как на горизонтальной плоскости. Математическим вычислением найдено, что такая кривая поверхность есть поверхность особого геометрического тела – параболоида. Ее можно получить, если быстро вращать вокруг вертикальной оси стакан, до половины налитый водой: тогда вода у краев поднимется, в центре опустится, и поверхность ее примет форму параболоида.
Если вместо воды налить в стакан растопленный воск и продолжать вращение до тех пор, пока воск не остынет, то затвердевшая поверхность его даст нам точную форму параболоида. При определенной скорости вращения такая поверхность является для тяжелых тел как бы горизонтальной: шарик, положенный в любую ее точку, не скатывается вниз, а остается на этом уровне (рис. 36).
Теперь легко будет понять устройство «заколдованного» шара.
Дно его (рис. 37) составляет большая вращающаяся платформа, которой придана кривизна параболоида. Хотя вращение благодаря скрытому под платформой механизму совершается чрезвычайно плавно, все же люди на платформе испытывали бы головокружение, если бы окружающие предметы не перемещались вместе с ними; чтобы не дать возможности наблюдателю обнаружить движение, платформу помещают внутри большого шара с непрозрачными стенками, который вращается с такой же скоростью, как и сама платформа.
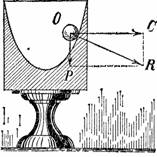
Рисунок 36. Если этот бокал вращать с достаточной скоростью, то шарик не скатится на его дно.
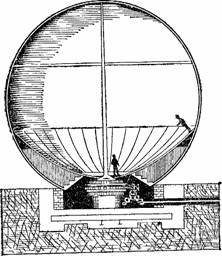
Таково устройство этой карусели, носящей название «заколдованной» или «волшебной» сферы. Что же испытываете вы, находясь на платформе внутри сферы? Когда она вращается, пол под вашими ногами горизонтален, в какой бы точке кривой платформы вы ни находились, – у оси, где пол действительно горизонтален, или у края, где он наклонен на 45°. Глаза ясно видят вогнутость, мускульное же чувство свидетельствует, что под вами ровное место.
Показания обоих чувств противоречат друг другу самым резким образом. Если вы перейдете с одного края платформы на другой, то вам покажется, будто весь огромный шар с легкостью мыльного пузыря перевалился на другой бок под тяжестью вашего тела: ведь во всякой точке вы чувствуете себя, как на горизонтальной плоскости. А положение других людей, стоящих на платформе наклонно, должно представляться вам до крайности необычайным: вам буквально будет казаться, что люди, как мухи, ходят по стенам (рис. 39).
Вода, вылитая на пол заколдованного шара, растеклась бы ровным слоем по его кривой поверхности. Людям казалось бы, что вода здесь стоит перед ними наклонной стеной.
Привычные представления о законах тяжести словно отменяются в этом удивительном шаре, и мы переносимся в сказочный мир чудес…
Подобные ощущения испытывает на поворотах летчик. Так, если он летит со скоростью 200 км в час по кривой с радиусом 500 м, то земля должна казаться[16] ему приподнявшейся и наклоненной на 16°.

Рисунок 38. Истинное положение людей внутри «заколдованною» шара.

Рисунок 39. Положение, которое представляется при этом каждому из двух посетителей.
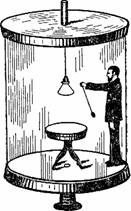
Рисунок 40. Вращающаяся лаборатория – действительное положение.
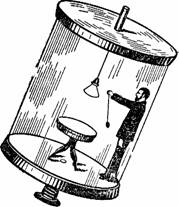
В Германии, в городе Геттингене, была сооружена для научных изысканий подобная вращающаяся лаборатория. Это (рис. 40) цилиндрическая комната 3 м в поперечнике, вращающаяся со скоростью до 50 оборотов в секунду. Так как пол комнаты плоский, то при вращении наблюдателю, стоящему у стены, кажется, будто комната откинулась назад, а сам он полулежит на покатой стене (рис. 41).
Жидкий телескоп
Наилучшая форма для зеркала отражательного телескопа – параболическая, т. е. именно та форма, какую сама собою принимает поверхность жидкости во вращающемся сосуде. Конструкторы телескопов затрачивают много хлопотливого труда, чтобы придать зеркалу подобную форму. Изготовление зеркала для телескопа длится целые годы. Американский физик Вуд обошел эти затруднения, устроив жидкое зеркало: вращая ртуть в широком сосуде, он получил идеальную параболическую поверхность, которая могла играть роль зеркала, так как ртуть хорошо отражает лучи света. Телескоп Вуда был установлен в неглубоком колодце.Недостаток телескопа, однако, тот, что малейший толчок морщит поверхность жидкого зеркала и искажает изображение, а также и тот, что горизонтальное зеркало дает возможность непосредственно рассматривать только те светила, которые находятся в зените.
«Чертова петля»
Быть может, вам знаком головокружительный велосипедный трюк, иногда исполняемый в цирках: велосипедист едет в петле снизу вверх и описывает полный круг, несмотря на то, что по верхней части круга ему приходится ехать вниз головой. На арене устраивают деревянную дорожку в виде петли с одним или несколькими завитками, как изображено на нашем рис 42. Артист спускается на велосипеде по наклонной части петли, затем быстро взлетает на своем стальном коне вверх, по круговой ее части, совершает полный оборот, буквально вниз головой, и благополучно съезжает на землю[17].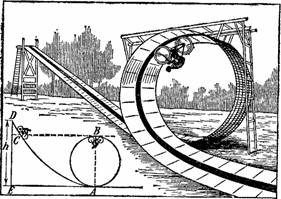
Этот головоломный велосипедный фокус кажется зрителям верхом акробатического искусства. Озадаченная публика в недоумении спрашивает себя: какая таинственная сила удерживает смельчака вниз головой? Недоверчиво настроенные готовы подозревать здесь ловкий обман, а между тем в трюке нет ничего сверхъестественного. Он всецело объясняется законами механики. Биллиардный шар, пущенный по этой дорожке, выполнил бы то же с не меньшим успехом. В школьных физических кабинетах имеются миниатюрные «чертовы петли».
Знаменитый исполнитель и изобретатель этого трюка, артист «Мефисто», для испытания прочности «чертовой петли» имел тяжелый шар, вес которого равнялся весу артиста вместо с велосипедом. Шар этот пускали по дорожке петли, и если он благополучно пробегал ее, то артист решался проделать петлю сам.
Читатель, конечно, догадывается, что причина странного явления – та же, которая объясняет общеизвестный опыт с вращающимся ведерком (стр. 55). Однако трюк удается но всегда; необходимо в точности рассчитать высоту, с которой велосипедист должен начать свое движение: иначе трюк окончится катастрофой.
Математика в цирке
Я знаю, что ряды «бездушных» формул отпугивают иных любителей физики. Но, отказываясь от знакомства с математической стороной явлений, такие недруги математики лишают себя удовольствия заранее предусматривать ход явления и определять его условия. В данном, например, случае две-три формулы помогут нам в точности определить, при каких условиях возможно успешное выполнение столь удивительного трюка, как пробег в «чертовой петле».Приступим же к расчетам.
Обозначим буквами те величины, с которыми придется вести расчеты:
буквой h обозначим высоту, с которой скатывается велосипедист;
буквой х обозначим ту часть высоты h, которая возвышается над верхней точкой «петли»; из рис. 42 очевидно, что x = h – АВ;
буквой г обозначим радиус круга петли;
буквой m – общую массу артиста вместе с велосипедом; вес их выразится тогда через mg, причем:
буквой g обозначено ускорение силы земной тяжести; оно равно, как известно, 9,8 м/с за секунду;
буквой v обозначим скорость велосипеда в тот момент, когда он достигает самой верхней точки круга.
Все эти величины мы можем связать двумя уравнениями. Во-первых, мы знаем из механики, что скорость, которую приобретает велосипед к моменту, когда, катясь по наклонной дорожке, он находится в С на уровне точки В (это положение изображено в нижней части на рис. 42), равна той, какую он имеет в верхней части петли, в точке В. Первая скорость выражается формулой
Расчет этот не учитывает влияния силы трения в велосипеде: считается, что скорости в точке С и точке В одинаковы. Поэтому нельзя слишком удлинять путь и делать очень отлогий спуск. При отлогом спуске в результате действия трения скорость велосипеда по достижении точки В будет меньшей, чем в точке С.
Надо заметить, что при исполнении этого трюка велосипедист едет без цепи, предоставляя машину действию тяжести: ни ускорять, ни замедлять своего движения он не может, да и не должен. Все его искусство в том, чтобы держаться середины деревянной дорожки; при малейшем уклонении артист рискует съехать с дорожки и быть отброшенным в сторону. Скорость движения по кругу весьма велика: при круге с поперечником 16 м ездок совершает оборот в 3 секунды. Это соответствует скорости 60 км в час! Управлять велосипедом при такой скорости, конечно, мудрено; но этого и не надо; можно смело положиться на законы механики. «Сам по себе велосипедный трюк, – читаем мы в брошюре, составленной профессионалом, – при правильном расчете и прочной конструкции аппарата не опасен. Опасность трюка лежит в самом артисте. Если рука артиста дрогнет, если он будет взволнован, потеряет самообладание, если ему неожиданно сделается дурно, то можно ожидать всего».
На этом же законе покоится всем известная «мертвая петля» и другие фигуры высшего пилотажа. В «мертвой петле» первостепенную роль играет правильный «разгон» пилота по кривой и умелое управление самолетом.
Нехватка в весе
Какой-то шутник объявил однажды, что знает способ без обмана обвешивать покупателей. Секрет состоит в том, чтобы покупать товары в странах экваториальных, а продавать – поближе к полюсам. Давно известно, что близ экватора вещи имеют меньший вес, нежели близ полюсов; 1 кг, перенесенный с экватора на полюс, прибавится в весе на 5 г. Надо пользоваться, однако, не обыкновенными весами, а пружинными, притом изготовленными (градуированными) на экваторе, иначе никакой выгоды не получится: товар станет тяжелее и на столько же тяжелее сделаются гири. Если купить тонну золота где-нибудь в Перу, а сбыть ее, скажем, в Исландии, то можно, пожалуй, на этом кое-что заработать, – при бесплатном провозе, разумеется.Не думаю, чтобы подобная торговля могла кого-нибудь обогатить, но по существу шутник прав: сила тяжести действительно увеличивается с удалением от экватора. Происходит это оттого, что тела на экваторе описывают при вращении Земли самые большие круги, а также и оттого, что земной шар как бы вздут у экватора.
Главная доля недостачи веса обусловлена вращением Земли; оно уменьшает вес тела близ экватора на 1/290 долю по сравнению с весом того же тела у полюсов.
Разница в весе при переносе тела с одной широты на другую для легких тел ничтожна. Но для предметов грузных она может достигнуть величины довольно солидной. Вы и не подозревали, например, что паровоз, весящий в Москве 60 тонн, по прибытии в Архангельск становится на 60 кг тяжелее, а по прибытии в Одессу – на столько же легче. В свое время с острова Шпицбергена ежегодно вывозили в более южные порты до 300 000 тонн угля. Если бы это количество было доставлено в какой-нибудь экваториальный порт, то там обнаружена была бы недостача в 1200 тонн, будь груз перевешен при приемке на пружинных весах, вывезенных со Шпицбергена. Линкор, весивший в Архангельске 20 000 тонн, по прибытии в экваториальные воды становится легче тонн на 80; но это остается неощутимым, так как соответственно становятся легче и все другие тела, не исключая, конечно, и воды в океане[19].
Если бы земной шар вращался вокруг своей оси быстрее, чем теперь, например, если бы сутки длились не 24 часа, а, скажем, 4 часа, то разница в весе тел на экваторе и полюсах была бы заметна резче. При четырехчасовых сутках, например, гиря, весящая на полюсе 1 кг, весила бы на экваторе всего 875 г. Именно таковы приблизительно условия тяжести на Сатурне: близ полюсов этой планеты все тела на 1/6 тяжелее, чем на экваторе.
Так как центростремительное ускорение возрастает пропорционально квадрату скорости, то нетрудно вычислить, при какой скорости вращения оно на земном экваторе должно стать в 290 раз более, т. е. сравняться с силой притяжения. Это наступит при скорости, в 17 раз большей, нежели нынешняя (17*17 – почти 290). В таком состоянии тела перестанут оказывать давление на свои опоры. Другими словами, если бы Земля вращалась в 17 раз быстрее, вещи на экваторе совсем не имели бы веса! На Сатурне это наступило бы при скорости вращения, всего в 2, 5 раза большей, чем нынешняя.